Lattice dynamics of KI perturbed by Jahn-Teller centres

Lattice dynamics of KI perturbed by Jahn-Teller centres

The theoretical study of the physical properties of JT centres (impurities, defects, etc. )embedded in a crystal is usually done in the framework of the cluster model [I]. In such a model the localized electron of the centre, which is in a degenerate state by definition of the JT effect, is assumed to interact only with a single localized vibrational mode, any lattice dispersion of frequency being neglected. This model is known to take into account several important features of the JT induced properties [I] but not the details of the optical spectra (Raman, infrared, vibronic sidebands of the absorption/emission spectra), which are very sensitive to the dynamics of the host crystal.

In a recent paper [2] the problem of the lattice dynamics perturbed by a JT centre was studied and resolved in the weak interaction limit by using the Green function method. It was found that a JT centre generates a very peculiar perturbation on the dynamical matrix.

On the other hand, a similar result can be obtained when the absorption lineshape due to a singletmultiplet transition (the dynamic JT effect) is studied. In this case the JT perturbed lattice dynamics is that relative to the excited electronic degenerate state. In both cases we conclude that the JT interaction induces a perturbation on the force constant matrix, which can be eventually seen in the structures of the phonon densities. Such a result, which will be presented in details in a forthcoming paper, can be deduced in the limit of the weak interaction from the absorption lineshape theory proposed some years ago (ref. [3] hereafter called MT).
In the present paper, after some consideration on the previous point, we present the computed one-phonon spectra for a (e x E) JT centre. As usual, (e x E) means that the electron is in a e-symmetry degenerate state and interacts with the E-symmetry displacements of the neighbour ions. Our aim is to see to what extent the JT dynamical perturbation can qualitatively modify the host lattice dynamics. So we do not apply it to any real impurity.
In the following we assume : 1) The JT centre is embedded in an ionic crystal. 2) The JT interaction is weak. 3) Only the n.n. of the JT centre are involved in the JT interaction.

The shape of the optical spectra is related to the symmetrized (E-symmetry in this case) projected phonon density p,(w) relative to the lattice dynamics, either of the ground electronic state (Raman and infrared spectra), or of the excited electronic state (vibronic sidebands). We remember that p,(o) is given by the imaginary part of the E-symmetry phonon propagator DE(a). So we first show the relevant JT induced processes which dress the unperturbed onephonon
propagator, and then we evaluated p,(o) from D,(o). By unperturbed propagator we mean the onephonon propagator when all the dynamical perturbations induced by the centre (change of mass and of force constants) are considered, but the JT interaction. It follows that the usual separation of the total Hamiltonian H in three terms (JT electron He, perturbed lattice HL and their interaction He,) can be used :

1) The electronic JT eigenfunctions and eigenvalues are evaluated in the static lattice and the electron is assumed to be in a doubly degenerate stationary state, whose energy E, falls in the host crystal energy gap. Such a state is either the ground state or the excited state, depending on the problem.

2) HL is the lattice Hamiltonian in the harmonic approximation, given by

Here I labels the ions in the crystal (I = 0 indicates the position of theJT centre) ; A,,. = A;. + 6A,,. is the force constant matrix of the perturbed lattice (the perturbation 6A,,. is zero for anisotopic centre); M, are the masses ; u, and p1 are the canonical dynamical variables (displacement u, and momentum p,). A labels the normal modes of the imperfect crystal whose frequency is on ; b, and b: are the annihilation and creation operators of a phonon on the A mode.

3) HeL is the JT interaction Hamiltonian. He, is usually written as follows

where u,, and u,, are the two E-symmetry combinations of the n.n. displacements of the JT centre; h(E1) = ox and h(E2) = - o,, where ox and o, are the Pauli matrices [I]. c is the coupling constant. HeL is very peculiar : it is localized both in the wavefunction space (He, # 0 only inside the degenerate e-space) and in the lattice space (only the n.n. of the JT centre interact with the electron). The complexity of the JT problem is immediately shown by evaluating the commutators of the electron and phonon operators entering He,, because :

i) He, does no commute with TL, because of the phonon operators ; [TL,H e =\ 0] This is the term which generates phonons (the so-called many-phonon process) also for normal impurities.

ii) The coupling coefficients h(E, i) are not commuting matrices : [h(E, 1), h(E,2) =\ 0]

iii) For the previous reason also

In the cluster model, where one assumes that only the n.n. of the centre are involved in HL, as they are in He,, only two degenerate E-symmetry modes with the same frequency are representative of the whole lattice dynamics. So the commutator (6) loses its meaning. From the properties of the commutators (4) and (5) one can see that, while the electron and the
phonons are truly independent when He, = 0, they are so entangled for HeL # 0 to determined new coupled states, the so-called vibronic states. When the vibronic states are studied in the cluster model, the role played by HeL on the electronic states is emphasized but the possible modifications of HL are neglected [I].

The opposite approach is here follow ed. In fact we compute the modifications of the one-phonon projected density of states pE(02), when the electron is supposed to be degenerate but structureless. Without the JT interaction, the unperturbed phonon propagator D;(t) (a dotted line in the diagram of figure 1) is given at T = 0 K by

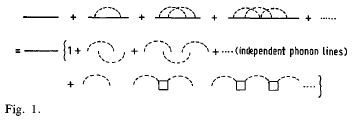
where p;(02) is the unperturbed projected one-phonon density. (By &(w2) we mean its Hilbert transform.) In the harmonic approximation a phonon does not change frequency when a linear electron-phonon interaction is switched on and the only effect is a generation of many unperturbed phonons. When the electron is in a degenerate state, since the usual separation of the phonons from the electron (adiabatic approximation) is not valid anymore, the linear JT interaction modifies the frequency of the phonons. By following MT [3], one can prove that in the diagrams accounting for the many-phonon process there is always a class of higher order graphs (the crossing graphs) which give a contribution to the lower order graphs, when the electron line is removed by assuming that the electron is structureless. We draw such graph in figure 1 and decompose them as it follows :

In the previous graphs the squares are the commutators (6), the full line is the electron propagator and the dotted lines are the phonon propagators (7). The series on the last row can be summed in the weak interaction limit and the dressed E-symmetry propagator DE(m2) can be evaluated [2]. Note that, owing to the matrix character of W,, in the e-space, also D,(02) is a 2 x 2 matrix, so one finds that the resulting JT perturbed projected density pE(w) is composed
by two parts ; &o), each corresponding to one of the values of the frequency dependent JT dynamical perturbation 6A, (m)

to examine both points and emphasize the influence of 6A, on p$(o), we computed p,'(w) also for values of Q,, outside the range of validity of the very weak interaction limit.
The difference in the values here found for the average frequency on the distributions p:(o) corresponds to the splitting of E7 (o = 15 f 2 QJT), which is found in the cluster model in the very weak interaction limit. The computed pg(o) confirm that the more intense the JT perturbation, the greater the difference between ~ : ( oan)d p, (o).

As regard to the structure of p$(o), we note that &A, causes two effects. 1) It can generate a low frequency resonance whose intensity and frequency goes to zero for 611, 4 0. No gap modes are found in KI. 2) It strongly modifies the host lattice frequency distribution pg(o), mainly in the acoustic region. ,Therefore, we can suggest on a qualitative basis that 'the structures found in the one-phonon part of the experimental optical spectra of the ST centres, should correspond either to JT resonances or to peaks in the host lattice density of states perturbed by dA,. Moreover, since such peaks are not predicted in the cluster model, one must be careful in using it for interpreting the optical spectra.